
The finite groups generated in this way are examples of Coxeter groups. In general, a group generated by reflections in affine hyperplanes is known as a reflection group. Similarly the Euclidean group, which consists of all isometries of Euclidean space, is generated by reflections in affine hyperplanes. In geometry, a reflection is a rigid transformation in which an object is mirrored across a line. Thus reflections generate the orthogonal group, and this result is known as the Cartan–Dieudonné theorem. Every rotation is the result of reflecting in an even number of reflections in hyperplanes through the origin, and every improper rotation is the result of reflecting in an odd number. The product of two such matrices is a special orthogonal matrix that represents a rotation. The matrix for a reflection is orthogonal with determinant −1 and eigenvalues −1, 1, 1. Point Q is then the reflection of point P through line AB. P and Q will be the points of intersection of these two circles. Step 2 (green): construct circles centered at A′ and B′ having radius r.Step 1 (red): construct a circle with center at P and some fixed radius r to create points A′ and B′ on the line AB, which will be equidistant from P.
To reflect point P through the line AB using compass and straightedge, proceed as follows (see figure): To find the reflection of a figure, reflect each point in the figure. In a plane (or, respectively, 3-dimensional) geometry, to find the reflection of a point drop a perpendicular from the point to the line (plane) used for reflection, and extend it the same distance on the other side. Once we find that line, it shows how one triangle reflects onto the other. reflection, reflectional symmetry, line of reflection, transformation, function.
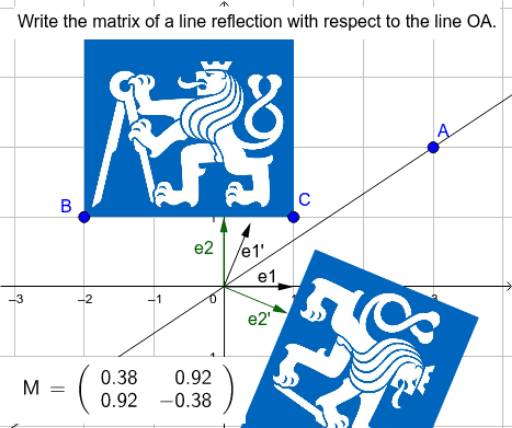
All of the halfway points are on the line. We find this line by finding the halfway points between matching points on the source and image triangles. Construction Point Q is the reflection of point P through the line AB. A line of reflection is an imaginary line that flips one shape onto another. Some mathematicians use " flip" as a synonym for "reflection". Typically, however, unqualified use of the term "reflection" means reflection in a hyperplane. Other examples include reflections in a line in three-dimensional space. In a Euclidean vector space, the reflection in the point situated at the origin is the same as vector negation. What is a Line of Reflection Just about everything in math has a name Did you know that the line you reflect a figure over has a special name It's called the line of reflection Watch this tutorial and learn about the line of reflection. This operation is also known as a central inversion ( Coxeter 1969, §7.2), and exhibits Euclidean space as a symmetric space. For instance a reflection through a point is an involutive isometry with just one fixed point the image of the letter p under it Such isometries have a set of fixed points (the "mirror") that is an affine subspace, but is possibly smaller than a hyperplane. The term reflection is sometimes used for a larger class of mappings from a Euclidean space to itself, namely the non-identity isometries that are involutions. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state. Its image by reflection in a horizontal axis (a horizontal reflection) would look like b. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis (a vertical reflection) would look like q. The image of a figure by a reflection is its mirror image in the axis or plane of reflection.

In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points this set is called the axis (in dimension 2) or plane (in dimension 3) of reflection. For reflexivity of binary relations, see reflexive relation. This tells us that the coordinate of the reflected point is \((9,12)\).This article is about reflection in geometry. So to get the reflected point \(P'\), we must add \(3\) to the \(x\)-coordinate and \(4\) to the \(y\)-coordinate of \(M(6,8)\), as illustrated below: We can see that the difference in \(x\)-coordinates between \((3,4)\) and \((6,8)\) is \(3\), and the difference in \(y\)-coordinates is \(4\). We must now use this information to find the reflected point. (So in terms of vectors, \(\overrightarrow x = 50,\] that is, \ Then substituting this into either equation gives \(y = 8\), so \(M\) lies at \((6,8)\). The point \(P(3,4)\) and its reflection \(P'\) in the line \(L\) are related in two ways: the line \(PP'\) is perpendicular to the line \(L\), and \(P\) and \(P'\) are equidistant (equal distances) from \(L\). Let \(L\) be the line with equation \(3x + 4y = 50\). What is the reflection of the point \((3,4)\) in the line \(3x + 4y = 50\)?


 0 kommentar(er)
0 kommentar(er)
